Chia đều tờ giấy trong origami – the art of Origami

Giới thiệu về origami

Từ Origami đơn giản là sự kết hợp giữa Ori (折り) là gấp/xếp và Kami (紙) là giấy. Nên Origami (折り紙) có thể hiểu đơn giản là một loại hình xếp giấy có xuất sứ từ Nhật Bản. Trong Origami, những tờ giấy 2 chiều (thường là hình vuông), thông qua các nếp gấp đơn giản mà không cần cắt dán, có thể biến thành nhiều hình thù 3 chiều đẹp mắt và thú vị.

Chia đều tờ giấy – bước khởi đầu trong Origami

Trong origami, những bước gấp nếp đầu tiên rất đối quan trọng. Việc gấp nếp giúp chia phần tờ giấy, tạo ra những phần tỉ lệ phù hợp với kích thước của kết quả mong muốn. Các nếp gấp cũng tạo ra các đường mờ trên tờ giấy, tạo thành điểm tựa để gấp ở các bước phức tạp hơn. Việc gấp nếp có thể đơn giản như gấp đôi tờ giấy, gấp đường chéo cho đến những nếp phức tạp hơn như chia 7 tờ giấy, …

Chia đôi tờ giấy

Đây có vẻ là bước mà hầu như ai cũng biết. Việc chia đôi tờ giấy hình vuông rất đơn giản. Để chia theo chiều ngang/dọc, ta chỉ cần xếp sao cho 2 cạnh đối diện nhau trở nên trùng khớp. Ta hoàn toàn có thể chứng minh tính đúng đắn của cách xếp này về mặt toán học. Vì 2 cạnh được xếp trùng khớp nên khoảng cách của chúng đến đường gấp ở giữa phải là như nhau, từ đó chia đôi tờ giấy.

Từ cách thức chia đôi tờ giấy, ta có thể chia tiếp cho các lũy thừa của 2 (vd 4, 8, 16). Gấp cạnh sao cho trùng với đường gấp giữa ta sẽ được 1/4 tờ giấy, gấp cạnh trùng vào nếp gấp 1/4 sẽ được 1/8 và cứ thế tiếp tục.

Chia ba tờ giấy

Chia đôi đơn giản và được sử dụng rất nhiều vì hầu hết các mẫu vật cần gấp thường có tính đối xứng. Tuy nhiên cũng không ít trường hợp chúng ta cần chia tờ giấy theo một tỉ lệ phức tạp hơn và điển hình là chia ba.

Chia tờ giấy thành ba phần tưởng chừng đơn giản nhưng lại có một chút phức tạp nhất định. Trực giác của chúng ta dễ dàng mường tượng được vị trí mà ta cần phải gấp nhưng sự ước lượng đó lại hoàn toàn không chính xác rất dễ gây ra sai số lớn. Sai số khi ước lượng sẽ càng rõ ràng khi đòi hỏi chia tờ giấy làm nhiều phần hơn như 7 phần, 11 phần. Một ý tưởng khác chính là đo chiều dài chính xác của cạnh và chia chiều dài đó để xác định vị trí cần gấp. Tuy nhiên sẽ gặp khó khăn khi các chiều dài không chia hết (vd chia tờ 10cmx10cm làm 3 phần). Vậy làm sao để chia ba tờ giấy một cách hiệu quả?

Origami chỉ cho ta một phương pháp đơn giản như sau:

• Gấp đôi tờ giấy theo hướng ngang để có được đường nếp EC
• Gấp nếp đường chéo AD
• Gấp nếp đường chéo BC
• BC và AD sẽ giao nhau tại một điểm F
• Gấp các đường song song với các cạnh và đi qua F sẽ chia tờ giấy thành 1/3

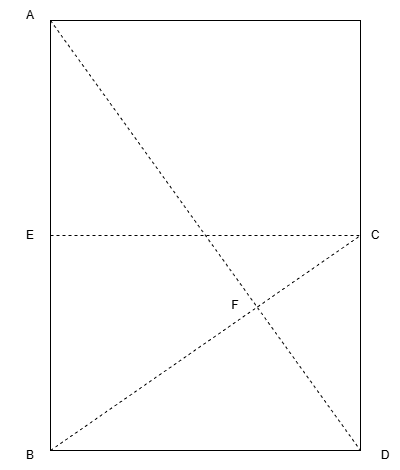
Thật vậy, ta có thể dễ dàng chứng minh điểm F sẽ giúp chia tờ giấy thành 3 phần. Ta có thấy được rằng tam giác ABF và CFD đồng dạng; và CD là một nửa AB vì ta gấp nếp EC là đường chia hai. Vì vậy BF = 2FC, và suy ra BC = 3FC. Đường song song với AB đi qua F cũng sẽ chia BD theo tỉ lệ FC/BC = 1/3. Như vậy ta đã có thể chia 3 tờ giấy.

Điểm đáng chú ý là cách làm này đúng với tờ giấy kích thước bất kỳ (bao gồm cả giấy hình vuông) nên được sử dụng trong bất kỳ cách xếp giấy origami nào đòi hỏi cần chia tờ giấy làm 3 phần.

Chia làm 5 phần và mở rộng ra các số khác

Ta đã có thể chia 2, chia 3, chia 4 (dựa trên cách chia 2). Vậy thì chia năm thì sao? Cách thức cũng sẽ tương tự với cách chia 3 nhưng thay vào đó ta sẽ dựa trên đường gấp nếp chia 4. EC là đường gấp nếp chia 1/4 tờ giấy vì vậy AB = 4CD. Do đó BF = 4FC và từ đó ta có BC = 5FC.

Ta gấp các đường song song với cạnh AB đi qua F sẽ chia BD theo tỉ lệ 1/5 và từ đó chia tờ giấy theo tỉ lệ 1/5.

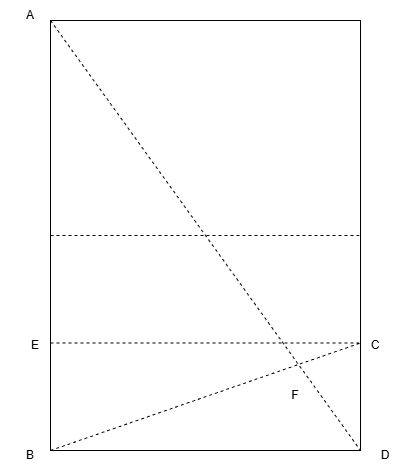
Ta thấy được rằng tỉ lệ giữa CD và AB chính là mấu chốt để tiến hành chia tờ giấy. Dựa trên cách thức này ta có thể chia theo bất kỳ tỉ lệ nào. Đúng hơn là ta sẽ quan tâm tới cách chia tờ giấy theo các số nguyên tố (2, 3, 5, 7, 11, …) còn đối với các hợp số ta sẽ tách chúng ra thành số nguyên tố rồi tiến hành chia tương ứng (ví dụ chia 6 thì sẽ tiến hành chia 2 rồi chia 3 phần đã chia 2).

Khi chia các số nguyên tố, ta cũng chỉ cần tách chúng ra thành các tổng của 1. Ví dụ:

• 3 = 2 + 1 (tiến hành chia 2 để có AB=2CD và từ đó tìm điểm F)
• 5 = 4 + 1 (tiến hành chia 4 để có AB=4CD và từ đó tìm điểm F)
• 7 = 6 + 1 (tiến hành chia 6 để có AB=6CD và từ đó tìm điểm F)
• ….

Như vậy, gần như ta có thể chia tờ giấy thành các tỉ lệ nào mà ta mong muốn, chỉ hơi khó khăn là phải tiến hành lấy nếp từ những cách chia trước đó. Nhưng một khi ta đã có những nếp gấp, bước tạo hình cho tờ giấy trong quá trình gấp sẽ đơn giản và chính xác hơn nhiều. Ta sẽ tạo ra được những mẫu gấp sinh động và tỉ lệ cân đối.