Tổng quan

Như đã trình bày trong bài viết "Não bộ xử lý thế giới như thế nào?", não bộ xử lý tín hiệu từ các giác quan thông qua một hệ thống mạng thần kinh gồm các tế bào nơ-ron. Các tế bào này liên kết với nhau thông qua xi-náp (synapse). Khi hai tế bào nơ-ron phát xung một cách đồng bộ, liên kết giữa hai tế bào này sẽ trở nên mạnh mẽ hơn, từ đó hình thành trí nhớ. Giống như việc nhìn thấy con mèo sau đó nghe tiếng "meo meo" lặp lại trong một thời gian nhất định sẽ hình thành liên kết giữa hai nơ-ron biểu diển hai khái niệm đó. Khi một tín hiệu mất đi (chỉ thấy con mèo), ta vẫn có thể tái xây dựng khái niệm về tín hiệu còn lại (thấy con mèo biết là nó sẽ kêu "meo meo"). Dựa trên cách thức hình thành liên kết này giữa hai nơ-ron, Donald Hebb đã đề xuất một luật học trong cuốn "The Organization of Behavior" vào năm 1949. Luật học này còn được biết đến với tên gọi Hebb's rule hay Hebbian rule.

Hebb's rule có thể được gói gọn trong một câu đơn giản "Neurons fire together wire together", tức là liên kết giữa những nơ-ron cùng bị kích hoạt sẽ được tăng cường và ngược lại, các nơ-ron bất đồng bộ sẽ có trọng số liên kết giảm xuống. Luật học có thể được thể hiện theo công thức

Wij=xixjW_{ij} = x_ix_j

Trong đó wijw_{ij} là giá trị trọng số giữa 2 nơ-ron. xi,xjx_i, x_j lần lượt là tín hiệu ra của nơ-ron i và j. Nếu hai nơ-ron đồng bộ, giá trị trọng số sẽ dương, ngược lại sẽ âm (trong trường hợp đầu ra nằm trong đoạn -1 tới 1). Trong trường hợp có nhiều mẫu học, trọng số sẽ được tính dựa trên trung bình của các mẫu học đó.

Wij=1p∑k=1pxikxjkW_{ij} = \frac{1}{p}\sum_{k=1}^{p}x_i^kx_j^k

Cách thức tính trọng số này được áp dụng trong mô hình mạng Hopfield. Ngoài ra, Hebb's rule còn có thể áp dụng theo các học dần trọng số bằng cách tính mức độ gia tăng trọng số như sau:

ΔWij=ηxiyjyj=∑iWijxi\Delta W_{ij} = \eta x_iy_j\\ y_j = \sum_{i}W_{ij}x_i

Như vậy, với một mẫu dữ liệu, trọng số sẽ được gia tăng nếu tín hiệu vào và tín hiệu ra đồng bộ. Sau nhiều lần quan sát các mẫu dữ liệu khác nhau, giá trị trọng số sẽ đạt đến ngưỡng chỉ cần một trong các yếu tố đầu vào tồn tại sẽ vẫn có thể kích hoạt được giá trị đầu ra. Tuy nhiên, công thức tính trên gặp phải một vấn đề về sự gia tăng ra vô hạn của trọng số. Nếu có quá nhiều mẫu học lặp đi lặp lại, những trọng số liên kết giữa các nơ-ron liên tục bị kích hoạt sẽ có thể tăng lên rất lớn, khiến cho chỉ cần duy nhất một nơ-ron kích hoạt cũng có thể kích hoạt các nơ-ron khác. Đặc biệt vấn đề này trở nên nghiêm trọng khi gặp phải các thuộc tính chung cho nhiều mẫu dữ liệu. Ví dụ như "mèo" và "chó" đều có 4 chân. Nếu trọng số của thuộc tính này quá lớn thì khi nơ-ron biểu diễn tính chất 4 chân bị kích hoạt thì nơ-ron biểu diễn "chó" cũng sẽ bị kích hoạt cho dù hình ảnh nhận vào là của lớp "mèo".

Oja's learning

Để hạn chế vấn đề về tính bất ổn định cũng như việc các trọng số có thể gia tăng quá lớn, Erkki Oja đã đề xuất một mô hình học cải tiến từ phương pháp của Hebb. Ý tưởng cải tiến ban đầu khá đơn giản, giản lược giá trị trọng số (normalizing) để độ dài vector biểu diễn trọng số luôn là 1 như sau:

wi(n+1)=wi+ηyxi(∑j=1m[wj+ηyxj]p)1/pw_i(n+1) = \frac{w_i + \eta yx_i}{(\sum_{j=1}^{m}[w_j + \eta yx_j]^p)^{1/p}}

Với điều kiện giá trị η\eta nhỏ, công thức cập nhật có thể lược giản thành như sau cho mô hình một nơ-ron.

ΔW=ηy(x−yw)\Delta W = \eta y(\textbf{x} - y\textbf{w})

Kết quả thực nghiệm trên mô hình học Oja's learning cho thấy kết quả đầu ra của mô hình một nơ-ron sẽ hội tụ thành thành phần chính của dữ liệu (first principal component) với điều kiện trọng số được lược giản về kích thước 1 và tốc độ học η\eta giảm dần theo số lần lặp.

Dựa trên đặc tính này, mô hình học Oja được mở rộng thành một mô hình phân tích thành phần chính (Principal Component Analyser - PCA) với cách thức cập nhật như sau:

ΔWij=η(yixj−yi∑k=1iwkjyk)\Delta W_{ij} = \eta (y_ix_j - y_i\sum_{k=1}^{i}w_{kj}y_k)

Cách thức cập nhật này giúp cập nhật mô hình nhiều đầu ra thành các thành phần chính của dữ liệu. Khác với việc dùng Oja learning cho từng nơ-ron riêng lẻ, cách thức cập nhật này đảm bảo các đầu ra không cùng hội tụ về một thành phần chính.

Ứng dụng của phương pháp học dựa trên Hebb' rule

Phân tích thành phần chính (PCA)

Như đã mô tả, mô hình Oja learning, một cải tiến dựa trên hebb's rule, có thể được sử dụng để tiến hành phân tích thành phần chính của dữ liệu. Cứ mỗi mẫu học đưa vào, mô hình sẽ được cập nhật trọng số. Sau một thời gian huấn luyện, kết quả đầu ra sẽ là những thành phần chính của bộ dữ liệu.

Lấy tập dữ liệu hoa iris làm ví dụ. Trong bộ dữ liệu iris, mỗi mẫu dữ liệu gồm 4 đặc trưng là kích thước của các cánh hoa. Ta cần rút ra 2 thành phần chính từ 4 đặc trưng của mẫu dữ liệu. Ta xây dựng hàm cập nhật như sau

import numpy as np
def Oja_update(x, W):
    y = np.dot(x, W)
    delta_W = eta*np.dot((x - np.dot(W,y)).reshape(4,1), y.reshape(1,2))
    W += delta_W
    W = W/np.linalg.norm(W, axis=0)

Trong đó W là ma trận ánh xạ sang không gian mới với kích thước 4x2. Sau mỗi bước cập nhật, ta chuẩn hóa W về lại vector kích thước 1. Sau một thời gian huấn luyện, kết quả thu được như hình bên dưới. Có thể thấy mô hình dần hội dụ về các thành phần chính (có thể dễ dàng kiểm tra với kết quả của PCA thông thường dựa trên eigen vector và eigen value).

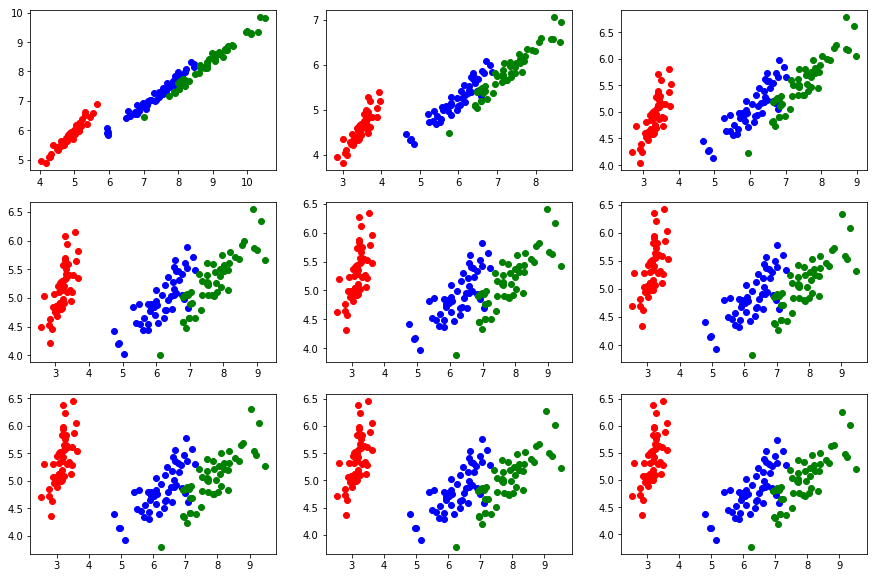
Sự thay đổi của đầu ra của mô hình sau các lần cập nhật (thay đổi dần từ trái qua phải, từ trên xuống dưới).

Phân lớp đối tượng

Mô hình học dựa trên Hebbian rule cũng có thể được áp dụng cho bài toán phân lớp. Giống như ý tưởng khởi nguồn của Hebb, những nơ-ron đầu vào sẽ tăng cường liên kết với các nơ-ron đầu ra nếu có sự kích hoạt đồng bộ. Khác với phương pháp dùng cho PCA, ta sẽ gán trực tiếp giá trị cho các nơ-ron đầu ra yy dựa trên nhãn của dữ liệu, sau đó cập nhật dựa trên công thức như ở mục trước.

Tiếp tục lấy ví dụ trong tập Iris, một mẫu có nhãn y=0y=0 sẽ được chuyển đổi thành y=[1,0,0]y = [1,0,0]. Tức là một nơ-ron đầu tiên bị kích hoạt còn 2 nơ-ron còn lại thì không. Như vậy, trong quá trình huấn luyện, các đặc trưng có giá trị cao sẽ được tăng trọng số liên kết với đầu ra kích hoạt tương ứng. Sau quá trình huấn luyện, các trọng số này có thể đủ lớn để kích hoạt nút đầu ra tương ứng.

Trước khi bắt đầu huấn luyện, ta cần tiến hành rút trích đặc trưng cho tập dữ liệu iris. Ta có thể áp dụng phương pháp mờ hóa (fuzzy) giá trị kích thước của cánh hoa theo các hàm mờ dài, ngắn, trung bình. Cụ thể như sau.

def iris_preprocess(x):
    x1 = x/np.max(x, axis=0) #long
    x2 = 1 - x1 #short
    x3 = 1 - np.abs(x1-0.5) #average
    result = np.concatenate((x1, x2, x3), axis=1)
    return result

Sau quá trình tiền sử lý, 4 đặc trưng của một mẫu dữ liệu iris sẽ chuyển thành 12 đặc trưng mờ tương ứng. Ví dụ một mẫu dữ liệu có đặc trưng [0.6455,0.7954,0.2028,0.08,0.3544,0.2045,0.7971,0.92,0.8544,0.7045,0.7028,0.58][0.6455, 0.7954, 0.2028, 0.08, 0.3544, 0.2045, 0.7971, 0.92, 0.8544, 0.7045, 0.7028, 0.58]; 4 giá trị đầu thể hiện mức độ dài của từng cánh hoa, giá trị càng cao nghĩa là cánh đó càng dài so với mức trung bình của hoa iris; 4 giá trị sau thể hiện tính chất ngược lại, càng cao khi cánh hoa càng ngắn; 4 giá trị cuối càng cao khi cánh hoa càng gần giá trị trung bình. Hàm mờ ở đây được cài đặt khá đơn giản. Có nhiều hàm mờ chuẩn xác hơn như dựa trên phân phối chuẩn.

Sau khi rút trích đặc trưng của dữ liệu, ta có thể tiến hành huấn luyện như sau.

def hebian_update(x, y, W):
    x = x.reshape(x.shape[0],1)
    y = y.reshape(1, y.shape[0])
    delta_W = 0.01*np.dot(x - np.dot(W,y.transpose()), y)
    W += delta_W
    W /= np.linalg.norm(W, axis=0)

Trong đó giá trị y là nhãn của dữ liệu như đã nêu ở trên. Sau quá trình huấn luyện, ta sẽ thu được bộ trọng số dùng để phân lớp. Ta phân lớp một mẫu dữ liệu mới như sau.

pred = np.argmax(sigmoid(np.dot(x, W)), axis=1)

Kết quả sau 5 lần duyệt qua bộ dữ liệu iris cho ra độ chính xác trên 95%. Ta cũng có thể kiểm chứng tính hiệu quả thông qua quan sát giá trị của W. Các giá trị W dùng để dự đoán nhóm y=0y=0 có 4 giá trị đầu thấp và 4 giá trị sau cao, thể hiện hoa nhóm thứ nhất có nhiều cánh nhỏ và trung bình. Trong khi đó giá trị trọng số của nhóm y=2y=2 có 4 giá trị đầu cao, thể hiện đây là những hoa cánh lớn.

Fast weight learning

Mô hình học dựa trên hebbian rule cũng được áp dụng trong một số công trình gần đây. Điển hình chính là mô hình fast weight learning. Song song với việc dùng slow weight learning (dựa trên gradient descent thông thường), hebbian rule cũng được dùng với tên gọi fast weight learning với việc nhanh chóng điều chỉnh mô hình trong trường hợp dữ liệu ít hoặc dùng trong việc thích ứng mô hình với một tập dữ liệu mới.

Mã nguồn tham khảo:https://github.com/luongquocan196/Hebbian_Rule

Bài viết tham khảo từ các nguồn

https://en.wikipedia.org/wiki/Oja%27s_rule

https://en.wikipedia.org/wiki/Generalized_Hebbian_Algorithm

Using Fast Weights to Attend to the Recent Past